Letter to Editor

A New Linear Derivative of the Michaelis-Menten Equation

Please cite this article as follows: Zarei MA. A new linear derivative of the michaelis-menten equation. Avicenna J Med Biochem. 2024; 12(1):62-63. doi:10.34172/ajmb.2489

Dear Editor,

Years of experience in teaching biochemistry and enzymology courses, especially the discussion of enzyme kinetics, has enabled us to determine the kinetic parameters of enzymes, especially the Michaelis constant K_m and the maximum reaction speed V_max using various mathematical equations. These equations include the Michaelis-Menten equation and many of its linear derivatives such as Lineweaver-Burk, Woolf-Augustinsson-Hofstee (Eadie- Hofstee in some text books), Eadie-Scatchard, and Hanes-Woolf equations (1,2). However, it seems that none of the above linear graphs can directly and quickly calculate the kinetic parameters of the Michaelis constant K_m and the maximum reaction speed V_max from the line equation. This inspired us to think about a new linear derivative of the Michaelis-Menten equation, by which we can directly calculate the Michaelis constant K_m and the maximum reaction rate V_max from the equation of the graph line.

Considering the graphs of Woolf-Augustinsson-Hofstee (V₀ vs. V₀/[S₀]), Eadie-Scatchard (V₀/[S₀] vs. V₀), and Hanes-Woolf ([S₀]/V₀ vs. [S]), the need for a new plot can be felt, which shows the change in [S₀] vs. [S₀]/V₀. Therefore, a diagram was drawn and its equation was extracted. Accordingly, the path of its derivation from the Michaelis-Menten equation is as follows:

1. V_0 =(V_max [S₀])/K_m + [S₀],

2. V₀K_m + V₀[S₀] = V_max[S₀],

3. (V₀K_m)/V₀ + (V₀[S₀])/V₀ = V_max[S₀]/V₀,

4. K_m + [S₀] = V_max[S₀]/V₀,

5. [S₀] = V_max[S₀]/V₀ - K_m

In equation 5, which is related to the linear graph of changes of [S₀] against [S₀]/V₀, the value of the maximum reaction speed V_max is directly obtained from the slope of the graph and the line constant by changing the sign of Michaelis constant K_m. As an example, we considered a problem presented by Mikkelsen and Cortón (3).

The information in the first and second rows of Table 1 was obtained from an enzyme saturation experiment by the substrate, determine the values of Michaelis constant Km and the maximum reaction rate Vmax by drawing a diagram.

At first we convert the raw data to the form which can be used in Lineweaver-Burk (rows 3 and 4 of Table 1) and new method (rows 5 and 6 of Table 1).

After drawing the corresponding graphs (Figures 1a and 1b), the values of Michaelis constant K_m and the maximum reaction rate V_max can be calculated from the equation of the line of each graph.

Close

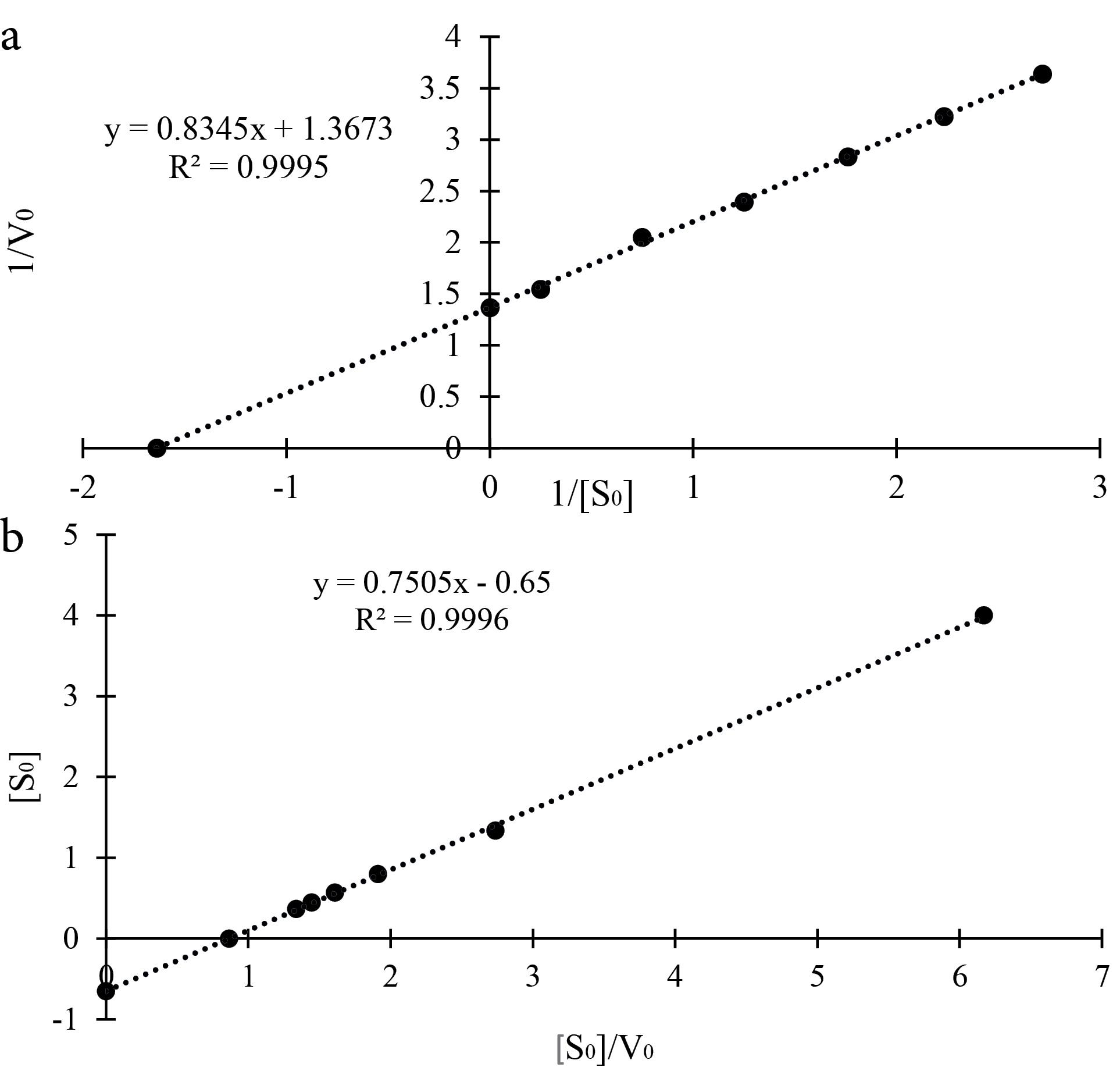
Figure 1.

a) Lineweaver-Burk Plot of Changes of 1/V₀ vs. 1/[S₀] b) New Plot, Changes of [S₀] vs. [S₀]/V₀

Figure 1.

a) Lineweaver-Burk Plot of Changes of 1/V₀ vs. 1/[S₀] b) New Plot, Changes of [S₀] vs. [S₀]/V₀

The line equation of the Lineweaver-Burk diagram is as follows:

1/V₀ = (K_m/V_max).1/[S₀] + 1/V_max

y = 0.8345x + 1.3673

As a result, 1/V_max = 1.3673, so V_max = 0.73 μmol/min.

On the other hand, K_m / V_max = 0.8345, as a result 0.73136 / K_m = 0.8345 and then K_m = 0.61 mM.

The equation of the line of the new graph is as follows:

[S₀] = V_max[S₀]/V₀ - K_m

y = 0.7505 x – 0.65

As a result, V_max = 0.75 μmol/min.

On the other hand, -K_m = -0.65, as a result, K_m = 0.65 mM.

The slight difference that was observed in the Michaelis constant K_m and the maximum reaction speed V_max obtained from the two approaches in the above working example is apparently caused by the unequal distance of the points due to the selection of certain concentrations of the substrate that are more suitable for the Lineweaver-Burk method. However, at non-selective concentrations of the substrate suitable for the Lineweaver-Burk plot, we can get more accurate results for the new method.

The new diagram can quickly give us the values of the Michaelis constant K_m and the maximum reaction speed V_max. The relation between this plot and the Hanes-Woolf plot is just similar to the relation between the Woolf-Augustinsson-Hofstee plot and the Eadie-Scatchard plot (1), in that we can go from one plot in the pair to the other just by changing the labels of y and x axes with each other. Therefore, the necessity of the proposed plot is equal to that of Woolf-Augustinsson-Hofstee plot. On the other hand, this plot is similar to the other three above-mentioned plots. However, in comparison with a double reciprocal plot like the Lineweaver-Burk plot, it is more straightforward in data analysis and result presentation.

A new single-reciprocal plot was derived from the Michaelis-Menten equation, which can be used for enzymatic analysis along with previous plots, and it is possible to directly calculate the K_m and V_max values from the equation of the plot without any additional mathematical operation.

Competing Interests

There is no competing interest.

Funding

None.

References

1. Segel IH. Biochemical Calculations. 2nd ed. John Wiley & Sons; 1976. p. 205-323.
2. Palmer T, Bonner PL. Enzymes: Biochemistry, Biotechnology, Clinical Chemistry. 2nd ed. Woodhead Publishing; 2007. p. 105-25.
3. Mikkelsen SR, Cortón E. Bioanalytical Chemistry. 1st ed. John Wiley & Sons; 2016. p. 83-60.